요약본 하나 만들어볼랬는데, 너무나 큰 귀찮음에 ㅈㅈ쳤다. 저거 만든사람 보통 정신력이 아니군.
필기자료 만드시고 공짜로 주시는 형님 글에서 기본값 하나 챙기자.
https://blog.naver.com/ttao00730/222200909835
정보처리기사 필기 - 정리본 pdf
2022년도, 최근에 들어서 비공개댓글로 실기 pdf를 보내달라는 방문자가 늘었습니다. 분명 저작권 문제로 ...
blog.naver.com
그리고 저기에 없고 최근 문제난이도 강화추세에 따라 나오는것 중에서도, 과정해설이 따로 필요한 것만 올린다.
이진 순서 문제: 1과목 트리순회, 2과목 스택 계산
제1과목 트리순회
(원래 - 없이 적는데, 영어 합성어 개념 알기쉬우라고 일부러 넣었다.)
일단 전중후 3종에선 root, left, right의 세가지 개념이 나오는데, 가독성 때문에 root = O로 표기한다.
이 개념은 연산자 표기법에도 똑같이 적용된다.
1. 근본 순서는 아래와 같다.
- 전위(pre-order) = OLR 순서. 동의어로 깊이우선순회=depth-first traversal
- 중위(in-order) = LOR 순서
- 후위(post-order) = LRO 순서
- 레벨(level-order) = 위에서 아래로 -> 왼쪽에서 오른쪽으로. 동의어는 너비우선순회=breadth-first traversal
2. 노드가 길면 비교대상 노드3개로만 만든다.
- 즉 그 하위노드를 모두 묶어서 하나의 노드처럼 생각하고 푼다.
- 아래 예제 순서도를 보면 괄호 안이든 밖이든 전부 순서를 지키는 걸 볼 수 있다.
3. 이제 문제로 익혀보자. (없는 노드는 공부할때 편하라고 x로 표기했다. )
| 기출 예제 (제1과목) | 방식(english) = 순서 | 결과 = 순서도해설 |
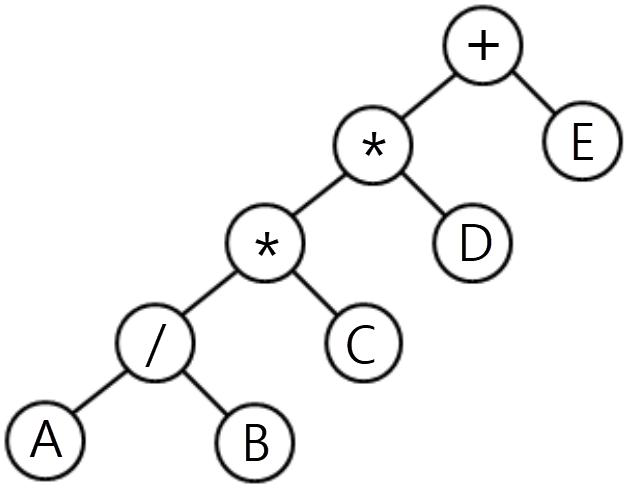 20-1+2, |
전위(pre-order) = OLR | + * * / A B C D E = + ->(* -->(* --->(/ A B) --->C) -->D) ->E |
| 중위(in-order) = LOR | A / B * C * D + E = + (((A / B) ->* C) -->* D) + E | |
| 후위(post-order) = LRO | A B / C * D * E + = (((A B /) ->C *) -->D *) E + | |
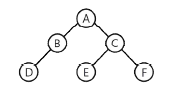 20-4, 21-3 |
전위(pre-order) = OLR | A B D C E F = A -> (B D x) -> (C E F) |
| 중위(in-order) = LOR | D B A E C F = (D B x) -> A -> (E C F) | |
| 후위(post-order) = LRO | D B E F C A = (D x B) -> (E F C) -> A | |
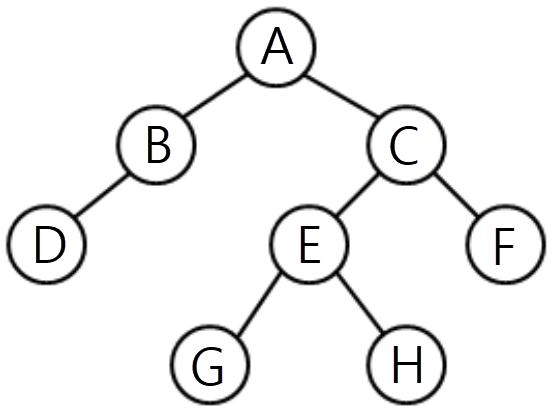 |
전위(pre-order) = OLR | A B D C E G H F = A -> (B D x) -> (C -->(E G H) -->F) |
| 중위(in-order) = LOR | D B A G E H C F = (D B x) -> A -> ( (G E H) -->C -->F) | |
| 후위(post-order) = LRO | D B G H E F C A = (D x B) -> ( (G H E) -->F -->C) -> A | |
| 레벨(level-order) | A B C D E F G H |
제2과목 식 계산 또는 식 변환
용어는 제1과목 -order 자리에 -fix 가 들어온다. 원리는 같다.
- 전위(pre-order) = OLR 순서 = (연산자, 값, 값)
- 중위(in-order) = LOR 순서 = (값, 연산자, 값)
- 후위(post-order) = LRO 순서 = (값, 값, 연산자)
계산은 쉽다. 이렇게 묶어서 괄호쳐주고 계산하면 끝. 작업이 끝난 괄호는 그 전체를 하나의 값으로 취급한다.
변환은 묶어서 괄호쳐준뒤 순서 바꿔준다. 괄호 처리는 마찬가지
| 회차 | 식 | 방식 | 과정 & 결과 |
| 20-4 | 3 4 * 5 6 * + | postfix 계산 | (3 4 * )(5 6 * )+ = 12 30 + = 42 |
| 21-1 | - / * A + B C D E | prefix to postfix | - (/ (* A (+ B C)) D) E = - (/ (* A (B C +)) D) E = - (/ (A (B C +) *) D) E = - ((A (B C +) *) D /) E = - ((A (B C +) *) D /) E = ((A (B C +) *) D /) E- = A B C + * D / E- |
정렬: 선택/삽입/버블. (회차 = PASS)
ㄱ. 삽입정렬(insertion sort)
- 초기자료의 첫번째 인덱스 건너뛰고, 두번째 인덱스부터 시작.
- 선택한 인덱스 앞의 모든 인덱스와 비교해서 순서 바꾸되, 앞 인덱스 값이 선택한 인덱스값보다 작으면 종료.
- 초기자료의 다음 인덱스(3번 4번 5번 ...)로 넘어가서 과정2번 반복.
20-4 의 제2과목
초기 자료 : 8, 3, 4, 9, 7
일단 첫번째 인덱스 값인 8은 제낀다.
1회차. 두번째 인덱스 값인 3을 그앞의 모든 자료(8뿐)와 비교하여 자리 바꿔준다.
-> 3, 8, 4, 9, 7 로 바뀐다.
2회차. 세번째 인덱스 값인 4를, 그앞의 모든 자료(3, 8)과 비교하여 자리 바꿔준다.
-> 3, 4, 8, 9, 7 로 바뀐다. (3이랑은 못바꾼다.)
3회차. 네번째 인덱스 값인 9를, 그앞의 모든 자료(3,4,8)과 비교하여 자리 바꿔준다.
-> 3, 4, 8, 9, 7 (그대로이다.)
4회차. 마지막 인덱스 값인 7을 앞에 모든 것과 비교
-> 3, 4, 7, 8, 9 (4랑은 못바꾼다.)
깔끔하게 정렬완료.
ㄴ. 선택정렬(selection sort)
- 주어진 리스트의 최소값을 선택한다.
- 그 값을 맨 앞에 위치한 값과 교체한다. (최소값이 맨앞값이면 동작하는순간 그회차 그대로 끝)
- 맨 처음 위치를 뺀 나머지 리스트를 같은 방법으로 교체하는걸 반복.
21-1 의 제2과목
초기 자료 : 8, 3, 4, 9, 7
1회차 8, 3, 4, 9, 7
-> 3 8 4 9 7
2회차 3 8 4 9 7
-> 3 4 8 9 7
3회차 3 4 8 9 7
-> 3 4 7 9 8
4회차 3 4 7 9 8
->3 4 7 8 9
ㄷ. 버블정렬(bubble sort)
- 모든 인덱스에 대해, i번째와 i+1번째를 묶어(bubble), 비교하여 필요시 위치를 바꾼다.
- 반복한다.
21-2 의 제2과목
초기 자료 : 9, 6, 7, 3, 5
1회차. (9 6) 7 3 5 → 6 (9 7) 3 5 → 6 7 (9 3) 5 → 6 7 3 (9 5)
→ 6 7 3 5 9
2회차. (6 7) 3 5 9 → 6 (7 3) 5 9 → 6 3 (7 5) 9 → 6 3 5 (7 9)
-> 6 3 5 7 9
3회차. (6 3) 5 7 9 → 3 (6 5) 7 9 → 4 5 (6 7) 9 → 3 5 6 7 9
-> 3 5 6 7 9
끝
'자격증 > 정보처리기사' 카테고리의 다른 글
| 정보처리기사 개정후 코드해석 문제들 해설집 별도모음: 21년3회~ (합격해서 작업 중단.) (0) | 2022.04.18 |
|---|---|
| 2022년 제1회 정보처리기사 필기: 기출문제+정답표시+해설집 (0) | 2022.04.16 |
| 정보처리기사 처음 도전하는 초보자용 가이드 (0) | 2022.02.27 |
| 2020년 1,2회차통합 기출 77번 해설 (0) | 2022.02.27 |
| 정보처리기사 준비시작 (0) | 2022.01.04 |