float64에서 0.1+0.2 는 0.3 이 아니지만 float32에서는 0.3인 이유를, 상세하게 해설: 부동소수점 계산식 과정 정리

아무도 해설은 제대로 안 달아놓고, 과정만 덜렁 설명해놨길래 찾아서 한글번역하고 직접 따라해서 확인했다.

인용 항목에 있는, 영문해설(원문)을 구글언어번역 버튼 눌러서 봐도 된다.

이 글은 PC 로 보는게 좋으며, 모바일 가독성이 엉망일 수 있다.

 

들어가기

단순 계산값은 아래와 같다. 반복되는 부분은 밑줄쳤다.

 

dec 0.1 == bin 0.0001100

dec 0.2 == bin 0.001100

dec 0.3 == bin 0.01001

 

IEEE 754 Standard 도 쓴다.

1. 부동소수점 표기: float64 (배 정밀도)에서

float64 == sign 1 + exponent 11 + fraction 52 == 부호 1 + 지수 11 + 가수 52

 

 ※ 각각의 소수점 연산 결과는 반올림된다.

가수 52자리(소수점 뒤 52번째 자리까지)를 적어보고 반올림까지 처리한다.

 

10진수 (decimal)	2진수(binary)   ※ 64비트 부동소수점의 digits는 52자리 실제로는 이어져 있으나 보기좋게 8자리씩 띄움.
0.1	1. 10011001 10011001 10011001 10011001 10011001 10011001 10011001 =1. 10011001 10011001 10011001 10011001 10011001 10011001 1010 2^(-4)
0.2	1. 10011001 10011001 10011001 10011001 10011001 10011001 10011001 =1. 10011001 10011001 10011001 10011001 10011001 10011001 1010 2^(-3)
0.3	1. 00110010 00110010 00110010 00110010 00110010 00110010 00110011  =1. 00110011 00110011 00110011 00110011 00110011 00110011 0011 2^(-2)
ㄷ. 둘을 부동소수점 연산으로 더한다. 1의자리 정수에 결과가 1이 나오도록 자릿수 맞춰주어 더하고, round 연산 수행한다.
dec ◐ 2^(-2)    0.1  ◐ 0. 01100110 01100110 01100110 01100110 01100110 01100110 0110 10 +0.2  ◐ 0. 11001100 11001100 11001100 11001100 11001100 11001100 1101 0 =sum◐ 1. 00110011 00110011 00110011 00110011 00110011 00110011 0011 10 =rnd  ◐ 1. 00110011 00110011 00110011 00110011 00110011 00110011 0100
ㄹ. 결론 최종값 rnd  와 저장된 0.3의 맨 끝자리가 0100 과 0011 로 차이나는 모습을 볼 수 있다. 다시말해, '0.1+0.2의 부동소수점 연산'과 '0.3의 부동소수점 값'이 다르다. 그러므로, 0.1+0.2 == 0.3 은 False 일 수밖에 없다. 이 차이는 2^(-2) 0. 00000000 00000000 00000000 00000000 00000000 00000000 0001 = 1.0 * 2^(-2 -52) = 2^(-54)

실제로 python을 돌려보면 그러하다.

0.1+0.2-0.3의 부동소수점 표기값(err)와 2의-54승 이 같다.

 

그리고 0.1+0.2 =rnd 값은,

유명한 0.30000000000000004 = 0.3+ 0.4*10^(-16)이 나온다.

0.30000000000000004 의 이진값

 

길게 표현하는 변환기나 식이 잘 없어서 대략적으로 계산했다.

0.3000 0000 0000 0000 4441 는 참고자료의 2진 to 10진 변환기에 rnd의 2진값 넣은 결과다. 반올림 결과가 같다.

0.2999 9999 9999 9999 889? 는 참고자료의 2진 to 10진 변환기로 0.3의 2진값 넣은 결과다. 

0.0000 0000 0000 0000 5551 = 5.551*10^-17은 위 두값의 차이로, 실제 2^(-54)와 매우 비슷하다.

2. 부동소수점 표기: float32 (단 정밀도)에서

float32 == sign 1 + exponent 8 + fraction 23 == 부호 1 + 지수 8 + 가수 23

 

 ※ 각각의 소수점 연산 결과는 반올림된다.

가수 23자리(소수점 뒤 23번째 자리까지)를 적어보고 반올림까지 처리한다.

 

10진수(decimal)	2진수(binary)   ※ 64비트 부동소수점의 digits는 52자리 실제로는 이어져 있으나 보기좋게 8자리씩 띄움.
0.1	1. 10011001 10011001 1001 1001 1001 =1. 10011001 10011001 1001 101 2^(-4)
0.2	1. 10011001 10011001 1001 1001 1001 =1. 10011001 10011001 1001 101 2^(-3)
0.3	1. 00110011 00110011 0011 0011 0011 =1. 00110011 00110011 0011 010 2^(-2)
ㄷ. 둘을 부동소수점 연산으로 더한다. 1의자리 정수에 결과가 1이 나오도록 자릿수 맞춰주어 더하고, round 연산 수행한다.
dec ◐ 2^(-2)    0.1  ◐ 0. 01100110 01100110 0110 0110 1 +0.2  ◐ 0. 11001100 11001100 1100 1101 =sum◐ 1. 00110011 00110011 0011 0011 1 =rnd  ◐ 1. 00110011 00110011 0011 010
ㄹ. 결론 최종값 rnd  와 저장된 0.3의 맨 끝자리가 010 으로 같다. 다시말해, '0.1+0.2의 부동소수점 연산'과 '0.3의 부동소수점 값'이 같다. 그러므로, 0.1+0.2 == 0.3 은 True 이다.

 

---

인용 및 참고자료 (모두 float64 만들때 썼다.)

Online Python converter: 이것저것 넣어서 간단히 실험하는 용

 

한글 해설

0.1+0.6 해설만 있고 0.1+0.2 해설은 생략되어 살짝 불친절

https://nybounce.wordpress.com/2016/06/30/ieee-754-0-1-0-2-0-30000000000000004-0-1-0-2-%E2%89%A0-0-3/

[IEEE 754] 0.1 + 0.2 = 0.30000000000000004? 0.1 + 0.2 ≠ 0.3?

 

영문 해설

가장 상세한 자료. 이 글을 보고 필요한 부분만 발췌 번역

https://qr.ae/pvwtdh

What's IEEE 754 double precision floating point format in math (according to Google)? If it's not true that (0.1 + 0.2) + 0.3 \n

 

decimal to binary converter 십진수를 이진수로 바꿔주는 변환기

이거 필요해서, 만든답시고 시간 낭비했는데 누군가가 잘 만들어놨다.

 

to 32bit binary

https://www.h-schmidt.net/FloatConverter/IEEE754.html

IEEE-754 Floating Point Converter

to 64bit binary 전체 64자리의 0 또는 1 값의 맨앞 12개는 부호와 지수부이므로 잘 보아야 한다.

https://www.binaryconvert.com/result_double.html?decimal=048046051048048048048048048048048048048048048048048048052 

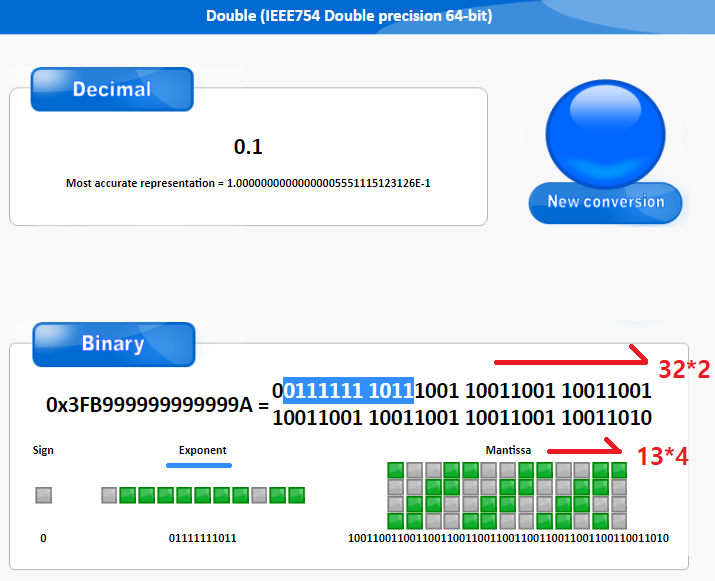
Double (IEEE754 Double precision 64-bit)

decimal to 64bit converter 사용시 주의.

 

binary to decimal converter

https://www.rapidtables.com/convert/number/binary-to-decimal.html

Binary to Decimal Converter